EWHADP Database: February 2014
|
This is the first issue of the EWHADP database (2014_02_25). It contains information about the location, time period, construction, size, and form of 1147 structures from 219 archaeological sites across eastern North America.
Basic Data Files Data are provided in Excel and JMP. The "Key to fields" file provides a short description of each field in the dataset.
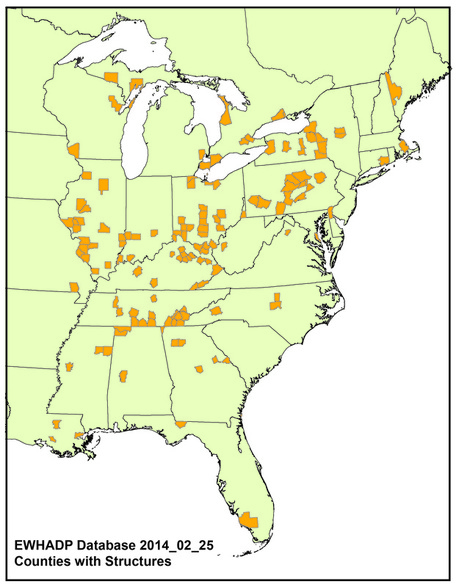
GIS Data Each structure in the database is associated with a county-level provenience. The figure to the right shows the distribution of counties/municipalities that contain prehistoric structures in the database. This figure was produced in ArcGIS by associating each structure with the UTM coordinates of the approximate center of the county/municipality in which the structure was located. The six files that constitute the ArcGIS shapefile are available below in a zipped folder. The UTM coordinates in the shapefile are in NAD 1983, Zone 16N. I had to remove the "Reference" column in order to create XY data because ArcGIS does not like colons. For future issues of the database, I'll create a field for references that does not contain page numbers. |
|
Number of Structures by Period
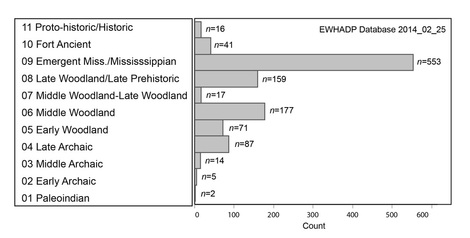
The database contains a field called "Period". The categories I used in this field assign each structure to a general time period and/or cultural-historical unit. Conventions of chronology and nomenclature used to sub-divide prehistoric time vary across eastern North America: the framework I used for the database is a general one that is intended to serve as a simple organizational tool. A variety of criteria were used to assign structures to periods, including radiocarbon dates pertaining to individual structures or other deposits at a site, associated diagnostic artifacts, stratigraphic associations, etc. Structures for which the period assignment is questionable are denoted by a "?" in the "Period_certainty" field of the dataset. The chart to the left shows the distribution of structures by period, including all structures assigned to a period regardless of functional interpretation or uncertainty about dates. |
|
Form
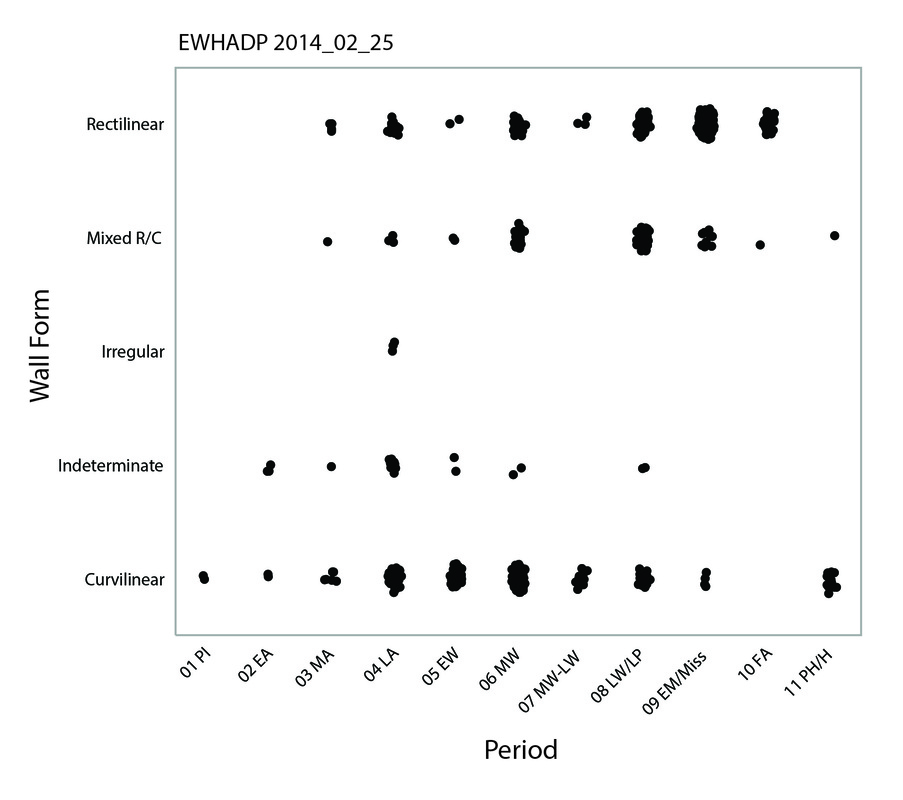
There are several fields in the database that code for aspects of construction, shape, and form. The work I have done so far with the structures in the database has not really considered architecture in any quantitative way, so I'm not satisfied that the information in these fields is as useful as it could be. I'm going to spend some time thinking about how to organize the database and define the fields to capture basic aspects of the construction and architecture of the structures in a consistent way. Any thoughts or suggestions would be helpful. The figure to the right shows the distribution of structures with curvilinear and rectilinear walls by period. Again, this figure was made utilizing all structures, regardless of functional interpretation. Rectilinear structures dominate the Mississippian period, of course, but have also been identified during most other periods of prehistory. |
|
Size
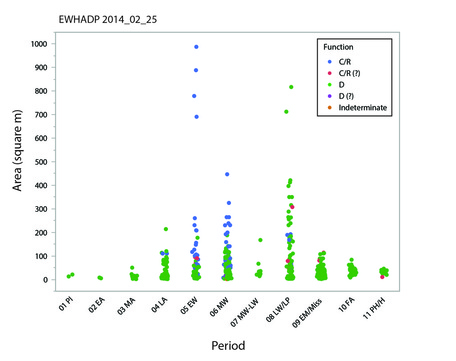
The database provides estimates of the enclosed area (in square meters) of structures when such an estimate was possible. The areas of circular structures were estimated by calculating the area of a circle with a given diameter. The areas of oval structures were estimated by calculating the area of a circle with a diameter equal to the mean of the "long" and "short" axes of the structure. The areas of rectangular and sub-rectangular structures were estimated by multiplying the length and width dimensions of the structure. Published floor area estimates were utilized when it was judged that these estimates were probably more accurate than those I could produce from maps or from the given dimensions of a structure. The figure to the left plots estimated structure sizes by period. The green points are structures that are coded in the database as "D" (i.e., "domestic"); the blue points represent structures coded as "C/R" (i.e., "communal/ritual"). The very large structures in the Early Woodland period are circular structures associated with Adena. The very large Late Woodland/Late Prehistoric domestic structures are longhouses. |
Some Thoughts on the First Issue of the Database
The goal of this project is to collect and disseminate data on prehistoric structures in a way that will be useful to a large number of people. After you've had a chance to look at the data and get a feel for the way the information is organized, let me know your thoughts on how it can be improved. As mentioned above, I'm interested in finding ways to consistently capture basic aspects of construction and architecture that are analytically useful. I would also like to get rid of the "Function" field: that was a field I used to exclude what I thought were non-domestic structures from the analysis in my JAA paper. It may be better to create a field or series of fields that describes the context of structural remains (e.g., sub-mound, supra-mound, open, etc.). I'm open to suggestions.
Suggested Citation
This version of the database should be cited as follows:
White, Andrew A. EWHADP Database 2014_02_25. Eastern Woodlands Household Archaeology Data Project, 25 Febrary 2014. Web (www.householdarchaeology.org). Accessed [day] [month] [year].
The goal of this project is to collect and disseminate data on prehistoric structures in a way that will be useful to a large number of people. After you've had a chance to look at the data and get a feel for the way the information is organized, let me know your thoughts on how it can be improved. As mentioned above, I'm interested in finding ways to consistently capture basic aspects of construction and architecture that are analytically useful. I would also like to get rid of the "Function" field: that was a field I used to exclude what I thought were non-domestic structures from the analysis in my JAA paper. It may be better to create a field or series of fields that describes the context of structural remains (e.g., sub-mound, supra-mound, open, etc.). I'm open to suggestions.
Suggested Citation
This version of the database should be cited as follows:
White, Andrew A. EWHADP Database 2014_02_25. Eastern Woodlands Household Archaeology Data Project, 25 Febrary 2014. Web (www.householdarchaeology.org). Accessed [day] [month] [year].